The term Algebra is derived from these two words; Alphabet
and Numbers. It is a combination of both Alphabet (letters) and Numbers.
Therefore, we can say that Alphabet + Numbers = Algebra and
Hence Alphabet + Numbers + Fractions = Algebra Fractions.
Types
of Algebra Fraction
There are two types of Algebra fractions;
, etc…
Rules for Solving Algebra Fractions
1. If the values are three digits, you factorise both numerator
and denominator.
2. If the values are two digits, you look for their common
factors.
3. If the values are single digit, just go ahead and simplify as
there’s no need to factorise or look for common factors!
Types
of Algebra Fractions
1. Simplification of Algebra Fractions
2. Multiplication & Division of Algebra Fractions
3. Substitution in Algebra Fractions
4. Equations in Algebra Fractions
1.
Simplification of Algebra Fractions
Examples; Simplify the following Algebra;
Solution
Step 1
Note;
The example above contains three digit values, am I right?
So we will factorise both the numerator and denominator before simplification;
NUMERATOR
a2 - 5a + 6 +6a2 (×) (-3a & -2a)
-5a (+)
a2 – 3a – 2a + 6
a(a – 3) -2(a – 3)
(a – 3) (a – 2)
Step 2
DENOMINATOR
2 – 3a + a2 (Rearrange)
a2 – 3a + 2 +2a2 (x) (-2a & -1a)
-3a (+)
a2 – 2a – 1a + 2
a (a – 2) -1(a – 2)
(a – 2)(a – 1)
Step 3
Bring the Numerator and Denominator together;
Step
4
Cancellation Process; (a – 2) cancels (a – 2);
Step
1
The example 2 above contains two digit values, so we will look
for common factors for both the Numerator and Denominator as well.
NUMERATOR;
6m2u2 - 4mu3 ---The common factor
is 2mu2.
2mu2(3m – 2u)
Step
2
DENOMINATOR;
9m3u – 4mu3 ---The common
factor is mu.
mu (9m2 – 4u2) ….this can also be written
thus as 32 gives 9 and 22 gives 4;
mu (32m2 – 22u2)
mu (3m – 2u)2 ….the “raise to power 2” has been
brought out as the common factor;
mu (3m – 2u)(3m + 2u)
Step
3
Combining the Numerator and Denominator;
Step
4
Cancellation Process; mu goes in 2mu2 to give 2u
while (3m – 2u) cancels each other;
Step
1
This is a three digit value, remember you factorise when dealing
with three digit values;
NUMERATOR;
a2 + ax – 6x2 -6a2x2 (×) (+3ax & - 2ax)
+ax (+)
a2 + 3ax – 2ax – 6x2
a(a + 3x) – 2x(a + 3x)
(a + 3x)(a – 2x)
Step
2
DENOMINATOR;
2x2 + ax – a2 (Rearrange)
- a2 + ax + 2x2 -2a2x2 (×) (+2ax & - 1ax)
+ax (+)
- a2 + 2ax – 1ax + 2x2
-a(a – 2x) – x(a – 2x)
(a – 2x)(-a – x)
Step
3
Combining the Numerator and Denominator;
Step
4
Cancellation Process; (a - 2x) cancels each other;
Note; The minus sign was brought out as a
common factor;
Note; The minus sign went up! This is a
rule as minus sign must always remain with the numerator;
Step
1
NUMERATOR;
ab + ac ----the common
factor will be a;
a(b + c)
Step
2
DENOMINATOR;
ad + ae -----the common
factor here will also be a;
a(d + e)
Step
3
Combining the Numerator and Denominator;
Step
4
Cancellation Process; a cancels each other;
Step
1
Note; The values above are single digit, so there’s no need for
factorization or common factors. Just go ahead and simplify!
Step
2
Cancellation Process; 2 goes in 8 gives 4 and 2 goes in 10 gives
5 while x goes in x2 gives x and z cancels z;




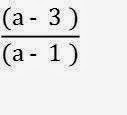














No comments:
Post a Comment